Predicting Housing Prices using Linear Regression

Introduction

In this session, we will learn how to predict housing prices using the Ames Housing dataset. The Ames Housing dataset contains 79 explanatory variables describing (almost) every aspect of residential homes in Ames, Iowa. Our objective is to predict the sale price of each home based on these variables using linear regression.

Loading the Data

First, let’s load the Ames Housing dataset into R.

library(tidyverse)
library(tidymodels)
library(caret)


ames <- read_csv("https://raw.githubusercontent.com/wblakecannon/ames/master/data/housing.csv")

# ames <- read.csv("./data/AmesHousing.csv")

head(ames)

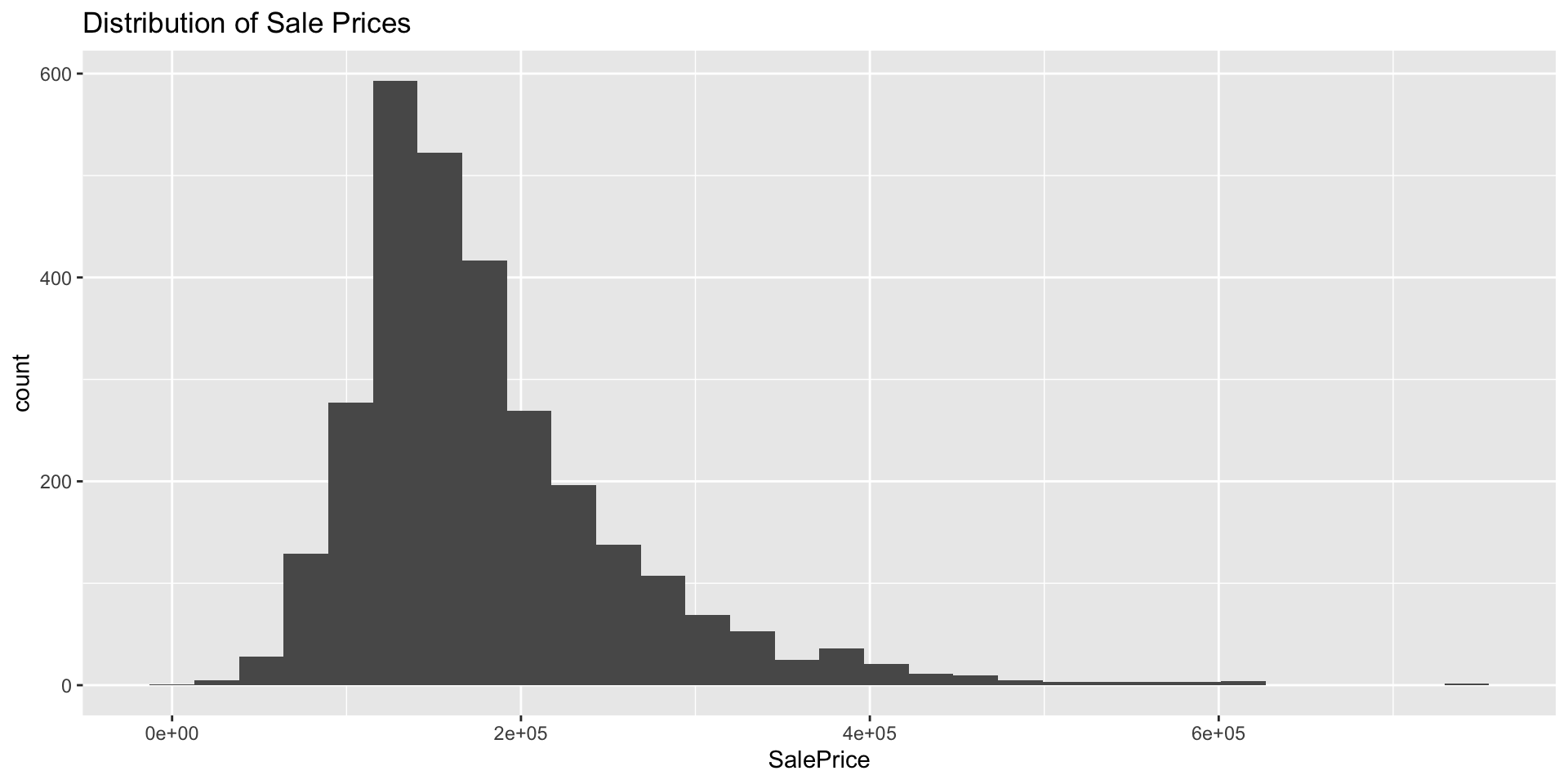
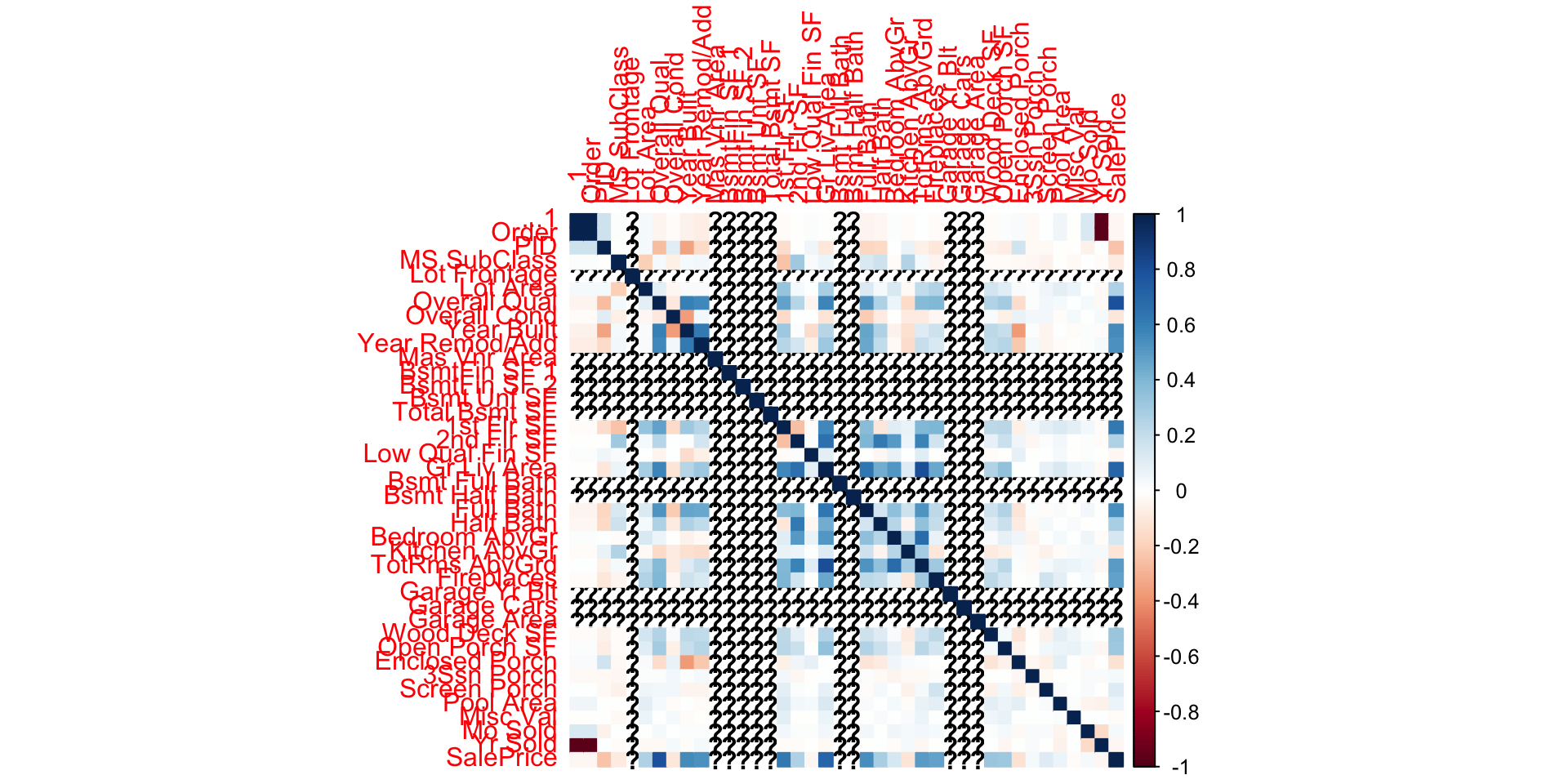
# A tibble: 6 × 83
   ...1 Order     PID `MS SubClass` `MS Zoning` `Lot Frontage` `Lot Area` Street
  <dbl> <dbl>   <dbl>         <dbl> <chr>                <dbl>      <dbl> <chr> 
1     0     1  5.26e8            20 RL                     141      31770 Pave  
2     1     2  5.26e8            20 RH                      80      11622 Pave  
3     2     3  5.26e8            20 RL                      81      14267 Pave  
4     3     4  5.26e8            20 RL                      93      11160 Pave  
5     4     5  5.27e8            60 RL                      74      13830 Pave  
6     5     6  5.27e8            60 RL                      78       9978 Pave  
# … with 75 more variables: Alley <chr>, Lot Shape <chr>, Land Contour <chr>,
#   Utilities <chr>, Lot Config <chr>, Land Slope <chr>, Neighborhood <chr>,
#   Condition 1 <chr>, Condition 2 <chr>, Bldg Type <chr>, House Style <chr>,
#   Overall Qual <dbl>, Overall Cond <dbl>, Year Built <dbl>,
#   Year Remod/Add <dbl>, Roof Style <chr>, Roof Matl <chr>,
#   Exterior 1st <chr>, Exterior 2nd <chr>, Mas Vnr Type <chr>,
#   Mas Vnr Area <dbl>, Exter Qual <chr>, Exter Cond <chr>, Foundation <chr>, …

Data Exploration

Before we start building our predictive model, let’s explore the Ames Housing dataset.

summary(ames$SalePrice)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  12789  129500  160000  180796  213500  755000 

ggplot(ames, aes(x = SalePrice)) +
  geom_histogram() +
  labs(title = "Distribution of Sale Prices")

Data Preparation

Before we can build our predictive model, we need to prepare the data by cleaning and transforming it.

correlation checks

# Select only numeric variables
ames_num <- ames %>% 
  select_if(is.numeric)

# Calculate correlation matrix
ames_corr <- cor(ames_num)

# Visualize correlation matrix
# Create a visualization of the correlation matrix
library(corrplot)

corrplot(ames_corr, method = "color")

# Data cleaning
ames_clean <- ames %>% 
  # Drop irrelevant columns
  select(-c( PID)) %>%
  # Remove outliers
  filter(SalePrice < quantile(SalePrice, 0.99)) %>%
  # Impute missing values
  mutate_if(is.numeric, ~ifelse(is.na(.), median(., na.rm = TRUE), .)) %>%
  mutate_if(is.character, ~ifelse(is.na(.), "Unknown", .))

pre-processing

ames_prep <- ames_clean %>% 
  # Scale numeric features
  mutate_if(is.numeric, scale) %>%
  # One-hot encode categorical features
  select(SalePrice, everything()) %>%
  mutate(across(where(is.character), as.factor)) %>%
  dummyVars(formula = ~., data = .) %>%
  predict(newdata = ames_clean) %>% 
  as.data.frame()# Use `newdata` parameter to transform the original `ames_clean` dataset

Feature selection

 ## the original `ames_clean` dataset

# Feature selection using RFE
X <- ames_prep[, -1]
y <- ames_prep[, 1]
lm_model <- train(SalePrice ~ ., data = ames_train, method = "lm")
rfe_model <- rfe(X, y, sizes = c(1:ncol(X)), rfeControl = rfeControl(functions = lmFuncs), method = "cv")
selected_features <- predict(rfe_model, X)
ames_selected <- ames_prep[, c(1, which(selected_features))]

# train_index <- createDataPartition(ames_selected$SalePrice, p = 0.8, list = FALSE)

Model Building

Now that we have prepared the data, let’s build our predictive model

# Model training
set.seed(123)
train_index <- train_index <- createDataPartition(ames_clean$SalePrice, p = 0.8, list = FALSE)

ames_train <- ames_prep[train_index, ]
ames_test <- ames_prep[-train_index, ]

lm_fit <- train(SalePrice ~ ., 
                data = ames_train, 
                method = "lm", 
                trControl = trainControl(method = "cv", number = 5, verboseIter = TRUE))

+ Fold1: intercept=TRUE 
- Fold1: intercept=TRUE 
+ Fold2: intercept=TRUE 
- Fold2: intercept=TRUE 
+ Fold3: intercept=TRUE 
- Fold3: intercept=TRUE 
+ Fold4: intercept=TRUE 
- Fold4: intercept=TRUE 
+ Fold5: intercept=TRUE 
- Fold5: intercept=TRUE 
Aggregating results
Fitting final model on full training set

# Here, we first set a random seed to ensure reproducibility of the results. 
# Then, we use the createDataPartition function from the caret package to split the data into training and testing sets.
# Next, we fit a linear regression model using the train function from caret. 
# We use 5-fold cross-validation to evaluate model performance and prevent overfitting.

lm_fit <- train(SalePrice ~ ., 
                data = ames_train, 
                method = "lm", 
                trControl = trainControl(method = "cv", number = 5, verboseIter = TRUE))

+ Fold1: intercept=TRUE 
- Fold1: intercept=TRUE 
+ Fold2: intercept=TRUE 
- Fold2: intercept=TRUE 
+ Fold3: intercept=TRUE 
- Fold3: intercept=TRUE 
+ Fold4: intercept=TRUE 
- Fold4: intercept=TRUE 
+ Fold5: intercept=TRUE 
- Fold5: intercept=TRUE 
Aggregating results
Fitting final model on full training set

# Here, we first set a random seed to ensure reproducibility of the results. 
# Then, we use the createDataPartition function from the caret package to split the data into training and testing sets.
# Next, we fit a linear regression model using the train function from caret. 
# We use 5-fold cross-validation to evaluate model performance and prevent overfitting.

Model Diagnostics

Let’s check the model assumptions and performance with diagnostic plots.

# Model evaluation

lm_preds <- predict(lm_fit, newdata = ames_test)
rmse <- sqrt(mean((ames_test$SalePrice - lm_preds)^2))

# Here, we make predictions using the test set and calculate the root mean squared error (RMSE) 
# to evaluate the performance of the model.

# Output results
cat("RMSE: ", rmse, "\n")

RMSE:  19349.06 

# Finally, we output the RMSE and a summary of the model's coefficients for interpretation.

Conclusion

In this session, we learned how to predict housing prices using the Ames Housing dataset in R using linear regression package. We explored the dataset, prepared the data, built a predictive model and tested it’s performance.